기록을

next permutation 기본형은 아래와 같다. 배열(벡터)의 다음 사전순 순서를 반환해준다.

1, 2, 3 ,4를 이용해서 만들 수 있는 모든 길이 4짜리 수열을 만드는 코드는 아래와 같다. (순서가 다르면 다른 수열)

#include<iostream>
#include<algorithm>
using namespace std;
int main(void) {
	int a[4] = { 1,2,3,4 };
	do {
		for (int i = 0; i < 4; i++)
			cout << a[i] << ' ';
		cout << '\n';
	} while (next_permutation(a, a + 4));
	return 0;
}

실행 결과는 위와 같다.

다음으로 6개의 숫자 중에서 2개의 숫자를 조합으로 뽑는 경우는 다음과 같다.

#include<iostream>
#include<algorithm>

using namespace std;
int main(void) {
	int a[6] = { 1,5,3,6,2,7 };
	//sort(a, a + 6);
	int Select[6] = { 0,0,1,1,1,1 }; //이러면 조합
	int cnt = 0;
	do {
		cnt++;
		for (int i = 0; i < 6; i++) 
			if (!Select[i]) cout << a[i] << ' ';
		cout << '\n';
	} while (next_permutation(Select, Select + 6));
	//cout << cnt;
	return 0;
}

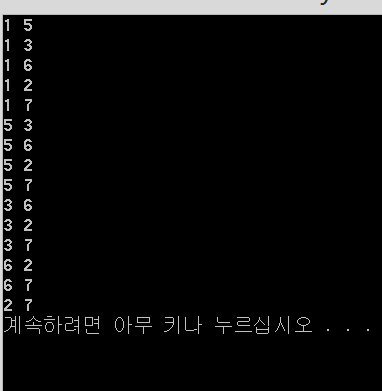
Select 배열을 가지고 next_permutation을 돌려준다. 뽑고 싶은 숫자의 개수를 0의 개수로 하고 앞에서부터 0을 써주면 된다. 위의 예시는 정렬을 하지 않았는데, 사용할 수 있는 숫자를 그대로 두고 실행했을 때 어떤 결과가 나오는지 보기 위함이다.

sorting하는 부분의 주석을 풀면, 사전순으로 수열이 정렬되서 나올 것이다.

이제 순열을 구현해보면 다음과 같다. 먼저 배열이 하나 더 필요하다. Select의 값이 0보다 클 때 if문에 진입하게 되고,

Select 값으로 index를 맞춰야 하는데 1부터 시작하므로 1씩 빼서 seq에 담아준 것이다. 

#include<iostream>
#include<algorithm>

using namespace std;
int main(void) {
	int a[6] = { 1,5,3,6,2,7 };
	//sort(a, a + 6);
	int Select[6] = { 0,0,0,0,1,2 }; 
	int cnt = 0;
	do {
		//cnt++;
		int seq[2] = {};
		for (int i = 0; i < 6; i++)
			if (Select[i]) seq[Select[i] - 1] = a[i];
		for (int i = 0; i < 2; i++) cout << seq[i] << ' ';
		cout << '\n';
	} while (next_permutation(Select, Select + 6));
	//cout << cnt;
	return 0;
}

https://www.acmicpc.net/problem/9663

퀸은 놓여있는 위치의 행과 열 그리고 대각선 두 방향을 공격할 수 있다.

N이 15 정도밖에 되지 않기 때문에 백트래킹을 해도 충분하다.

먼저 행당 1개의 퀸이 있는 것은 당연하다.

따라서 우리는 특정 열에 퀸을 놓을 수 있는가, 특정 대각선에 퀸을 놓을 수 있는가를 관리해주면 된다.

#include<iostream>
using namespace std;
int n;
bool isused[3][40];
int cnt = 0;
void func(int k) {
	//k-1개 까지 다 놓은 상태
	if (k == n + 1) {
		cnt++;
		return;
	}
	for (int i = 1; i <= n; i++) {
		if (isused[0][i] || isused[1][k + i] || isused[2][k - i + n - 1])
			continue;
		isused[0][i] = true;
		isused[1][k + i] = true;
		isused[2][k - i + n - 1] = true;
		func(k + 1);
		isused[0][i] = false;
		isused[1][k + i] = false;
		isused[2][k - i + n - 1] = false;
	}
}
int main(void) {
	cin >> n;
	func(1);
	cout << cnt;
	return 0;
}

https://www.acmicpc.net/problem/9663

퀸이 올라올 수 없는 곳의 위치를 체스판 한 칸 한 칸으로 관리하려고 했다.

그래서 2차원 배열을 활용했는데

초반의 생각은 이러했다.

가령 1,0에 퀸을 놓으면 1,0이 포함된 행과 열 그리고 두 개의 대각선에 퀸을 놀 수 없다.

이때 1,2는 둘 수 없는 위치이다. 그런데 2, 2는 둘 수 있는 위치이고, 2,2에 퀸을 두고 또 2,2를 둠으로써 둘 수 없는 위치를 잡고 나서 재귀를 빠져나올 때, 2,2의 행과 열 그리고 두 대각선의 bool 값을 모두 변경해버리면 1,1가 막고 있었던 것이 풀리게 되어서 제대로 된 연산이 되지 않는다.

따라서 좌표 하나하나를 관리할 게 아니라, 열과 행 그리고 대각선들로 사용중 여부를 관리하는 배열을 잡아야 한다.

#include<iostream>
using namespace std;
int N, m[15][15];
bool isused[15][15];
int cnt = 0;
void usage(int i, int j, bool ctr) {
	isused[i][j] = ctr;
	if (ctr) {
		printf("퀸위치: %d %d'\n", i, j);
	}
	for (int k = 0; k < N; k++) {
		isused[i][k] = ctr;
		isused[k][j] = ctr;
	}
	for (int l = 0; l < N; l++) {
		for (int m = 0; m < N; m++) {
			if (l + m == i + j) isused[l][m] = ctr;
			if (l - m == i - j) isused[l][m] = ctr;
		}
	}
}
void func(int k) {
	if (k == N+1 ) {
		cnt++;
		
		return;
	}
	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			if (!isused[i][j]) {
				usage(i, j, true);
				printf("%d %d에 퀸추가\n", i, j);
				for (int i = 0; i < N; i++) {
					for (int j = 0; j < N; j++) {
						cout << isused[i][j] << ' '; 
					}cout << '\n';
				}
				cout << '\n'<<'\n';
				func(k + 1);

				//isused[i][j] = false;
				usage(i, j, false);
				printf("%d %d에 퀸제거\n", i, j);
				for (int i = 0; i < N; i++) {
					for (int j = 0; j < N; j++) {
						cout << isused[i][j] << ' ';
					}cout << '\n';
				}
				cout << '\n' << '\n';
			}
		}
	}
}
int main(void) {
	cin >> N;
	func(1);
	cout << cnt << '\n';
	return 0;
}

https://www.acmicpc.net/problem/15664

사용할 수 있는 숫자들 중에 중복되는 숫자가 있을 수 있다.

숫자는 중복해서 사용하면 안 되고 입력받은 개수만큼만 사용해야 하며

만들어낸 수열은 비내림차순이어야 한다.

#include<iostream>
#include<vector>
#include<unordered_set>
#include<set>
using namespace std;
int N, M, arr[9], n[9];
bool isused[9];
set<vector<int> > st;
vector<int> v;
void func(int k) {
	
	if (k == M + 1) {
		for (int i = 1; i <= M; i++) {
			v.push_back(arr[i]);
		}
		st.insert(v);
		v.clear();
		return;
	}

	for (int i = 1; i <= N; i++) {
		if (!isused[i] && arr[k - 1] <= n[i]) {
			isused[i] = true;
			arr[k] = n[i];
			func(k + 1);
			isused[i] = false;
		}
	}
}
int main() {
	cin >> N >> M;
	for (int i = 1; i <= N; i++) {
		cin >> n[i];
	}
	func(1);
	for (set<vector<int> >::iterator it = st.begin(); it != st.end(); it++) {
		for (int i = 0; i < (*it).size(); i++) {
			cout << (*it)[i] << ' ';
		}
		cout << '\n';
	}
	return 0;
}

https://www.acmicpc.net/problem/2468

입력을 받으면서, 입력받는 높이의 최소와 최대를 구해둔다.

1부터 100까지 다 해볼 필요 없이 필요한 것만 해보는 것이다. 문제에서 아무 곳도 잠기지 않는 경우도 있다고 명시했기 때문에 높이 제한의 최소-1부터 최대까지를 물의 높이 변화로 정해주면 된다.

#include<iostream>
using namespace std;
int N, m[102][102];
bool vis[102][102];
int dr[4] = { 0,0,1,-1 };
int dc[4] = { 1,-1,0,0 };
void dfs(int row, int col, int H) {
	vis[row][col] = true;
	for (int i = 0; i < 4; i++) {
		int nr = row + dr[i];
		int nc = col + dc[i];
		if (nr < 0 || nc < 0 || nr >= N || nc >= N) continue;
		if (vis[nr][nc] || m[nr][nc] <= H) continue;
		dfs(nr, nc, H);
	}
}
void init() {
	for (int i = 0; i < N; i++)
		for (int j = 0; j < N; j++)
			vis[i][j] = false;
}
int main(void) {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cin >> N;
	int hMin = 110, hMax = -1;

	for (int i = 0; i < N; i++) {
		for (int j = 0; j < N; j++) {
			cin >> m[i][j];
			if (m[i][j] > hMax) hMax = m[i][j];
			if (m[i][j] < hMin) hMin = m[i][j];
		}
	}
	
	int cntMax = 0;
	for (int h = hMin - 1; h <= hMax ; h++) {
		int cntH = 0;
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				if (m[i][j] > h && !vis[i][j]) {
					dfs(i, j, h);
					cntH++;
				}
			}
		}
	
		if (cntH > cntMax) cntMax = cntH;
		init();
	}
	cout << cntMax << '\n';
	return 0;
}